Dem Martingalespiel, oder auch Martingale Roulette System, liegt der Wunsch zugrunde, einen Verlust durch einen höheren Einsatz und damit eventuell höheren Gewinn zu kompensieren.
Die einfache Martingale
 Die bekannteste Variante dieser Spielweise ist die einfache Martingale. Sie bezieht sich auf die einfachen Chancen und fordert nach einem Verlustcoup eine Verdoppelung des Einsatzes. Folgt ein Gewinncoup, so werden alle Verluste wieder ausgeglichen und es bleibt ein Stück als Gewinn.
Die bekannteste Variante dieser Spielweise ist die einfache Martingale. Sie bezieht sich auf die einfachen Chancen und fordert nach einem Verlustcoup eine Verdoppelung des Einsatzes. Folgt ein Gewinncoup, so werden alle Verluste wieder ausgeglichen und es bleibt ein Stück als Gewinn.
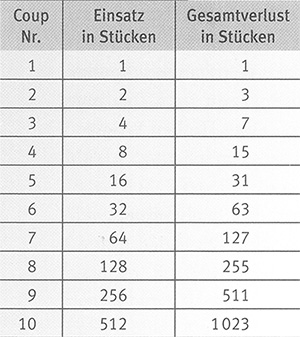
Dazu ein Beispiel: Der Spieler setzt auf Schwarz ein Stück. Erscheint Rot, setzt er danach zwei Stücke auf Schwarz. Erscheint dann Schwarz, hat er den ersten Verlust (ein Stück) ausgeglichen und erhält ein Stück als Gewinn. Im erneuten Verlustfall hingegen setzt er vier Stücke, und so geht es weiter. Man braucht nicht allzu viel Fantasie, auszumalen, wie schnell diese Progression in astronomische Höhen (repräsentiert durch das Tischmaximum) steigen kann. Die Tabelle zeigt, wohin die Progression nach nur zehn Stufen führen kann. Angesichts dieser Dimensionen ist es nicht weiter verwunderlich, dass unter Spielern gern von der „mörderischen Martingale“ gesprochen wird.
Auch die Literatur ist sich in dem Punkt einig, dass das Martingalespiel, besonders in seiner einfachen Form, eine äußerst gefährliche Sache ist. Trotzdem gibt es immer noch Spieler, die die Martingale bevorzugen, was wohl an der übersichtlichen Handhabung des Roulette Systems liegt.
 Für die Martingale ist es ohne Belang, wie hoch ein absoluter Ecart ist. Wichtig ist nur, dass die Höhe eines Zwischenecarts nicht die Anzahl der maximalen Progressionsstufen, die ein Spieler für sein Spiel festgelegt hat, übersteigen darf. Sobald ein für ihn negativer Ecart durch einen Gegenecart unterbrochen wird, beginnt der Spieler wieder von vorne, also im weitesten Sinne auch mit einer neu definierten Nulllinie.
Für die Martingale ist es ohne Belang, wie hoch ein absoluter Ecart ist. Wichtig ist nur, dass die Höhe eines Zwischenecarts nicht die Anzahl der maximalen Progressionsstufen, die ein Spieler für sein Spiel festgelegt hat, übersteigen darf. Sobald ein für ihn negativer Ecart durch einen Gegenecart unterbrochen wird, beginnt der Spieler wieder von vorne, also im weitesten Sinne auch mit einer neu definierten Nulllinie.
Berechnungen: Wenn Sie jetzt einwenden, dass zum Beispiel zehn aufeinanderfolgende Verlustcoups auf den einfachen Chancen äußerst unwahrscheinlich sind, so haben Sie sicherlich recht. Sollte es also doch so sein, dass durch das eine Gewinnstück pro Durchgang langfristig ein Gewinn zu erzielen ist? Um diese Frage zu beantworten, ziehen wir wieder die Mathematik zu Rate. Da wir Ihre Kapitalkraft nicht überstrapazieren wollen, begnügen wir uns mit einer Progression in höchstens fünf Stufen. Aus der Tabelle geht hervor, dass Sie dafür 31 Stücke als Spielkapital benötigen. Wir möchten nun also wissen, wie groß die Wahrscheinlichkeit ist, dass Sie fünfmal in Folge auf einer einfachen Chance einen Verlust und damit einen Platzer Ihrer Spielweise erleiden.
Von den 37 Roulettezahlen sind beim Satz auf einer einfachen Chance 18 günstig für uns. Das heißt, die Wahrscheinlichkeit, dass Sie auf einer einfachen Chance einen Treffer erlangen, beträgt 18/37. Die Wahrscheinlichkeit für einen Verlust beträgt demnach 19/37. (Um die Berechnungen zu vereinfachen, gehen wir hier davon aus, dass das Erscheinen der Null auch auf den einfachen Chancen grundsätzlich zum Verlust führen würde. Deshalb ist die Verlustwahrscheinlichkeit um ein Siebenunddreißigstel höher als die des Gewinnes.)
Nun interessiert uns die Wahrscheinlichkeit für fünf Verluste hintereinander. Vielleicht ist Ihnen aus der Schule noch bekannt, dass Chancen, die nacheinander ablaufen, multipliziert werden. Wir rechnen deshalb: 19/37 x 19/37 x 19/37 x 19/37 x 19/37 = (19/37)^5 = 0,0357
Da Wahrscheinlichkeiten in der Mathematik nicht als Teil von 100, sondern von 1 angegeben werden, müssen wir bei dem berechneten Wert nun noch das Komma um zwei Stellen nach rechts verschieben, um eine Prozentangabe zu erhalten. Das bedeutet, unsere Wahrscheinlichkeit für einen Totalverlust beträgt nur 3,57 % !
Das Martingale Roulette System in der Praxis
Sie könnten nun denken: Prima – wenn ich in 96,43 % der Fälle das Spiel mit einem Gewinn abschließe, spiele ich von nun an nur noch das einfache Martingalespiel! Doch leider ist das nur die halbe Wahrheit. Bedenken Sie, dass diese Spielweise nur Sinn macht, wenn sie einige Male hintereinander verfolgt wird. Oder wären Sie schon mit einem einzigen Gewinnstück zufrieden? Damit hätten Sie wohl noch nicht einmal den Eintritt und die Anreise finanziert. Spielen Sie das einfache Martingale System aber mehrmals, so werden Sie – früher oder später – von besagten 3,57% auf den Boden der Tatsachen zurückgeholt.
Bei 20 Durchgängen beträgt die Wahrscheinlichkeit, dass Sie keinen Platzer erleiden, nur noch (0,9643)^20 = 0,483, also 48,3 %!
Und dann wäre der Verlust auch gleich besonders hoch, nämlich 31 Stücke. Es bleibt die Frage, ob wir diese Jetons überhaupt durch eine gleich hohe Anzahl von Gewinndurchgängen wieder einspielen können. Auch das lässt sich anhand einer Rechnung überprüfen. Wir stellen uns vor, dass Sie 1000mal das einfache Martingale System mit einer Progression in fünf Stufen durchführen.
Der Hausvorteil und das Martingalespiel
Gemäß unseren Berechnungen erhalten Sie dann im statistischen Mittel 964mal einen positiven Ausgang (je ein Gewinnstück) und 36-mal einen negativen (je 31 Verluststücke). Sie bekommen also insgesamt 964 Gewinnstücke und 36 × 31 – 1116 Verluststücke. Die Bilanz fällt damit für Sie leider negativ aus. Sie fragen sich jetzt vielleicht, wie die Differenz zwischen diesen beiden Werten zustande kommt bzw. warum sie sich nicht genau ausgleichen.
Das ist allein auf die Banküberlegenheit durch die Null zurückzuführen. Wir rechnen das Beispiel
noch einmal durch, gehen nun aber davon aus, dass es keine Null gibt. Wir haben also bei jedem Coup eine Verlustwahrscheinlichkeit von 18/36. Die Wahrscheinlichkeit, fünfmal hintereinander einen Verlust zu erleiden, beträgt 0,031 bzw. 3,1%. In 1000 Versuchen haben wir also im Mittel 31,25 Verluste mit je 31 Stücken und 968,75 Gewinne von je einem Stück.
Die Bilanz ergibt insgesamt 31,25 x 31 = 968,75 Verluststücke und exakt genauso viele Gewinnstücke. Sie sehen also, dass der Ausgleich ohne die Banküberlegenheit gegeben wäre. Sicher ist nun auch klar, was mit dem Satz: „In jedem System spiegeln sich die Wahrscheinlichkeiten der einzelnen Chancen wider“.
Für den Gewinn ist es auch ohne Belang, in wie vielen Stufen die Progression durchgeführt wird. Das benötigte Kapital wächst jedoch mit einer längeren Progression sehr schnell. Je länger eine Progression weiterverfolgt wird, desto häufiger erhält man Gewinncoups, aber desto höher fällt auch ein Verlust aus. Wenn man von der Banküberlegenheit absieht, ist in jedem Fall der Ausgleich von Verlust und Gewinn gegeben.
Fazit zum Roulette Martingale System
Wir wollen nun einmal sehen, wie es einem Spieler ergangen wäre, der mit unserer Beispielpermanenz das einfache Martingale System mit fünf Progressionsstufen gespielt und dabei starr auf Schwarz gesetzt hätte. Sie sehen, dass bereits beim 20. Coup diese fünf Stufen nicht mehr ausgereicht hätten. Bei einem starren Spiel auf Rot hätte das System immerhin eine Haltbarkeit bis zum 56. Coup gehabt, bevor der erste Verlustdurchgang gekommen wäre.
Das Martingalespiel kann für die Praxis nicht empfohlen werden. Die Begründung liegt aber eher im psychologischen Bereich. Bedenken Sie, dass ein Roulette Spieler, der einen Verlustcoup erleidet, immer wieder den Mut aufbringen muss, für den nächten Coup nicht nur erneut zu setzen, sondern sogar einen noch höheren Einsatz zu riskieren. In dieser Situation kann er schnell dazu neigen, den Verlustausgleich „mit Gewalt“ erreichen zu wollen. Für das laufende Spiel ist das aber natürlich keine gute Ausgangslage.
Als Ergebnis unserer Berechnungen lässt sich für das Martingalespiel allgemein festhalten: Wir erhalten viele kleine Gewinne und wenige große Verluste. Abgesehen von der Banküberlegenheit gleichen sich beide langfristig genau aus.

